JEE 2014 :: Advanced 2014 :: Mathematics 2014

• Advanced 2014 - Physics 2014
• Advanced 2014 - Chemistry 2014
• Advanced 2014 - Mathematics 2014

 The function y=f(x)  is the solution of the differential equation $\frac{dy}{dx}+\frac{xy}{x^{2}-1}=\frac{x^{4}+2x}{\sqrt{1-x^{2}}}$   in (-1,1)

 satisfying f(0)=0, Then,   $\int_{-\frac{\sqrt{3}}{2}}^{\sqrt{3}/2} f(x) dx$  is

Answer:

Explanation:

 Plan 

 (i) solution  of the differential equation

 $\frac{dy}{dx}+Py=Q$  is 

 $Y.(IF)=\int_{}^{} Q.(IF) dx+c$

where,IF=$e^{\int P dx}$

(ii)$\int_{-a}^{a }f(x)dx=2\int_{0}^{a} f(x)dx,$

 if  f(-x)= f(x)

 Given differential  equation

$\frac{dy}{dx}+\frac{x}{x^{2}-1}y=\frac{x^{4}+2x}{\sqrt{1-x^{2}}}$

 This is a linear differential solution

 IF=   $e^{\int \frac{x}{x^{2}-1}dx}=e^{\frac{1}{2}ln|x^{2}-1|}$

                                          = $\sqrt{1-x^{2}}$

 $\Rightarrow$   Solution  is

$y\sqrt{1-x^{2}}=\int_{}^{} \frac{x(x^{3}+2)}{\sqrt{1-x^{2}}}.\sqrt{1-x^{2}}dx$

  or    $y\sqrt{1-x^{2}}=\int_{}^{} (x^{4}+2x) dx$

$=\frac{x^{5}}{5}+x^{2}=c$

    f(0)=0 $\Rightarrow$ c=0

  $\Rightarrow$      $f(x)\sqrt{1-x^{2}}=\frac{x^{5}}{5}+x^{2}$

 Now,    $\int_{-\sqrt{3}/2}^{\sqrt{3}/2}f(x) dx= \int_{-\sqrt{3}/2}^{\sqrt{3}/2}\frac{x^{2}}{\sqrt{1-x^{2}}}dx$

                                                                                                                         [using property]

 $=2\int_{0}^{\sqrt{3}/2}\frac{x^{2}}{\sqrt{1-x^{2}}}dx$

     $=2\int_{0}^{{\pi}/3}\frac{\sin^{2}\theta}{\cos\theta}\cos\theta d\theta$

                              [ taking x= sin $\theta$]

                $=2\int_{0}^{{\pi}/3}\sin^{2}\theta d\theta$

   $=\int_{0}^{{\pi}/3}(1-cos2\theta) d\theta$

   =  $\left(\theta-\frac{\sin 2\theta}{2}\right)_{0}^{\pi/3}$

  =  $\frac{\pi}{3}-\frac{\sin 2\pi/3}{2}$

          =  $\frac{\pi}{3}-\frac{\sqrt{3}}{4}$

The following integral    $\int_{\pi/4}^{\pi/2} (2 cosec$ $ x)^{17}$ is equal t

Answer:

Explanation:

 Plan  This type of question can be done using appropriate subsitiution

   Given,   $I= \int_{\pi/4}^{\pi/2} (2 cosec$ $x)^{17}$ dx

                    $2^{17}(cosec$ $x)^{16}$cosec$ x$

  $=\int_{\pi/4}^{\pi/2} \frac{(cosec x+cot x)}{(cosec x+cot x)}dx$

      Let $cosec$ $x +cot$ $x= t$

$\Rightarrow $   $ (-cosec$ $x.cot$ $x-cosec^{2}$ $x)$dx= dt

 and   $cosec$ $x-cot$ x=1/t

  $\Rightarrow 2cosec$ $x=t+\frac{1}{t}$

  $\therefore I= -\int_{\sqrt{2}+1}^{1} 2^{17}\left(\frac{t+1/t}{2}\right)^{16}\frac{dt}{t}$

  Let t= e^u   $\Rightarrow$  dt = e^u du. when t=1 

 e^u  =1

$\Rightarrow$

u=0

 and when  $t=\sqrt{2}+1,e^{u}=\sqrt{2}+1$ 

$\Rightarrow$     $u= ln(\sqrt{2}+1)$

$\Rightarrow$  $I=-\int_{ln(\sqrt{2}+1)}^{0} 2(e^{u}+e^{-u})^{16}\frac{e^{u}du}{e^{u}}$

=  $2\int_{0}^{ln(\sqrt{2}+1)}(e^{u}+e^{-u})^{16}du$

The common tangents to the circle  x²+y²=2 and the parabola  y²=8x  touch the circle at the points P, Q, and the parabola at the points  R, S. Then the area of the quadrilateral PQRS is

Answer:

Explanation:

Plan 

 (i) $y=mx+\frac{a}{m}$  is equation of tangent to the parabola y²=4ax

   (ii) A line is  atangent to circle , if distance of line from centre is equal to the radius of circle.

(iii)  Equation of chord drawn from exterior point (x₁,y₁) to a  circle/parabola is given by T=0

(iv)   Area of Trapezium= 1/2 ( sum of parallel sides) x ( distance  between them)

 Let equation  of tangent to parabola be

                    $y=mx+\frac{2}{m}$

 It also touches the circle x²+y²=2

$\therefore$     $ |\frac{2}{m\sqrt{1+m^{2}}}|=\sqrt{2}$

  $\Rightarrow$    $   m^{4}+m^{2}=2$

$\Rightarrow$    $  m^{4}+m^{2}-2=0$

$\Rightarrow$      $ (m^{2}-1)(m^{2}+2)=0$

$\Rightarrow$     $m=\pm 1,m^{2}=-2$     (m²  =-2 rejected)

 So , tangenth are y=x+2, y=-x-2, THey interset at (-2,0)

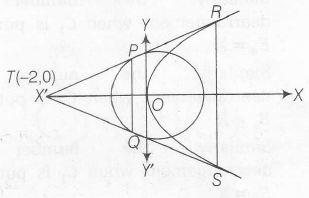
 Equation of chord PQ is, -2x=2

$\Rightarrow$        x=-1

Equation of chord RS is O =4(x-2)

$\Rightarrow$     x=2

    $\therefore$    Coordinates  of P,Q,R,S are

        P(-1,1), Q(-1,-1),R(2,4),S(2,-4) 

 Hence , are of PQRS =  $\frac{(2+8)\times3}{2}=15 $  sq.units

The quadratic equation p(x)=0 with real coefficients has purely imaginary roots. Then the equation p [p(x)]=0 has

Answer:

Explanation:

Plan  If quadratic equation has purely imaginary  roots, then coefficient of x must be  equal to zero

 Let p(x)= ax²+b  with a, b of same sign and $a,b \epsilon R$

 then p(p(x))= a(a x²+b)² +b

p(x)  has imaginary roots say ix

 Then, also ax²+b $\epsilon$   R

  and          (ax²+b)²  >0

 $\therefore$     $  a(ax^{2}+b)^{2}+b\neq0, \forall x$

 Thus     p[p(x)]  $\neq0, \forall x$

Six cards and six envelopes are numbered 1,2,3,4,5,6 and cards are to be placed in envelopes so that each envelope contains exactly one card and no card is placed in the envelope bearing the same number and moreover the card numbered 1 is always placed in envelope numbered 2. Then, the number of ways it can be done is

Answer:

Explanation:

 Plan  If there are n different objects  and n corresponding places, then the number of ways of  putting these  object to  the no object occupies its corresponding place

                   = $n!\left[\frac{1}{2!}-\frac{1}{3!}+....(-1)^{n}\frac{1}{n!}\right]$

 We have six cards C₁,C₂,C₃,C4,C₅,C₆

 and envelope E₁,E₂,E_3,E₄,E₅,E₆

Let the number of rearrangement when C₁  is put into E₂ =X

Similarly, the number of rearrangement when C₁  is put into E₃=X

Similarly, the number of rearrangement when C₁  is put into E₄=X

Similarly, the number of rearrangement when C₁  is put into E₅=X

Similarly, the number of rearrangement when C₁  is put into E₆=X

 Thus, total number of rearrangement =5X=D₆

 D₆= $6!\left[\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\frac{1}{5!}+\frac{1}{6!}\right]=265$

$\therefore$     $  X=265/5=53$

• Advanced 2014 - Physics 2014
• Advanced 2014 - Chemistry 2014
• Advanced 2014 - Mathematics 2014